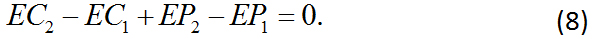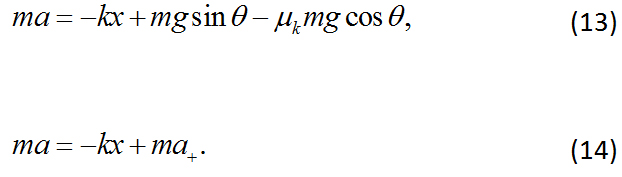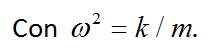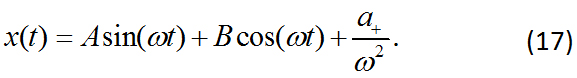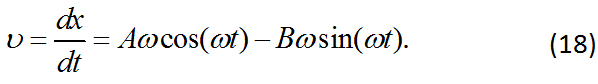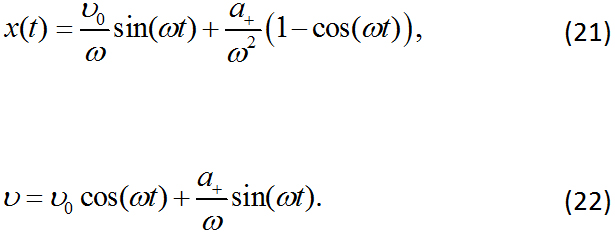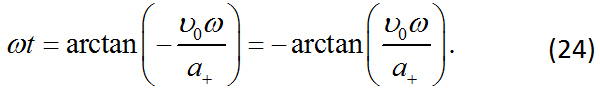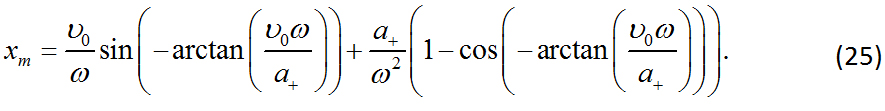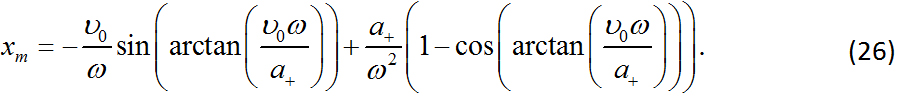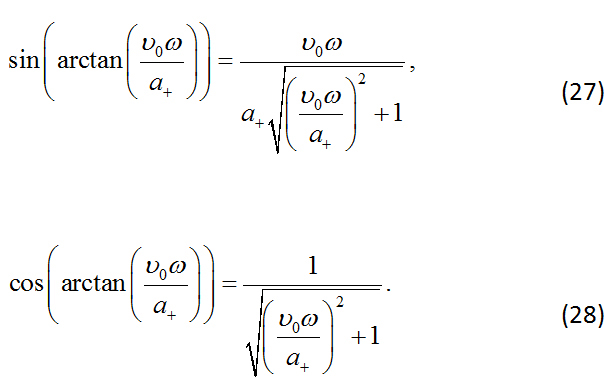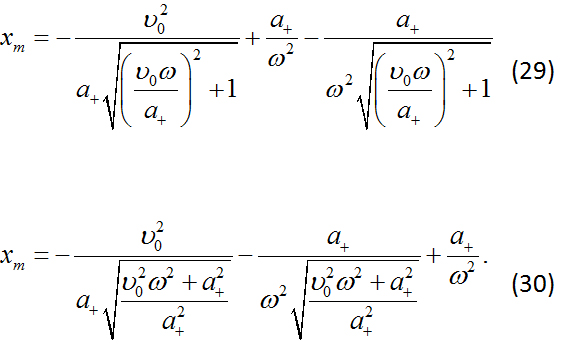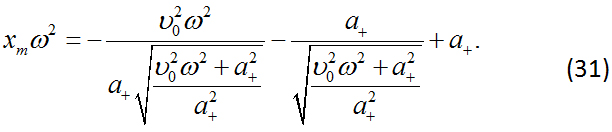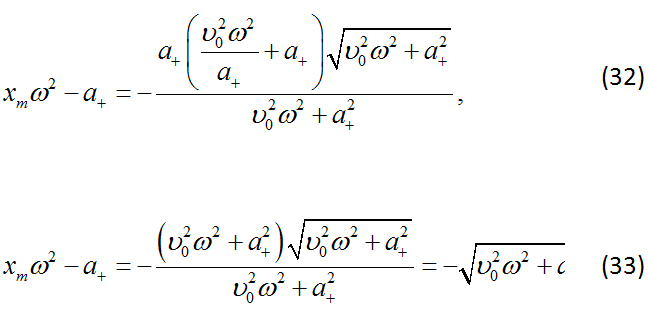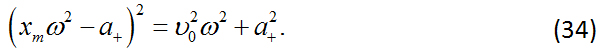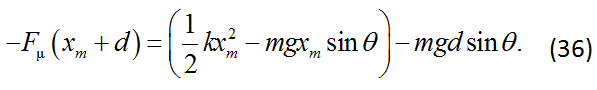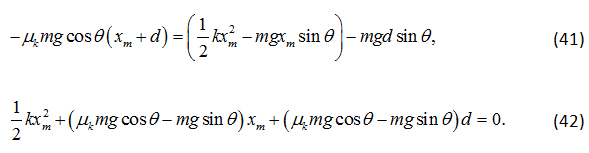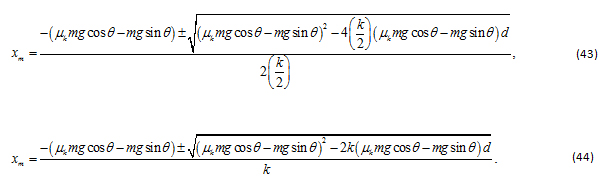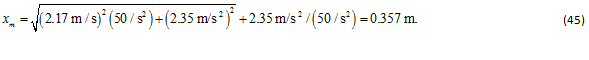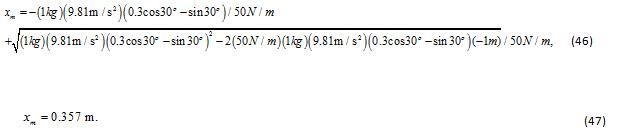Equivalencia entre las ecuaciones de movimiento de un sistema masa-resorte sobre un plano inclinado

A. Cruz Avilés^[a], Y. Muñoz Sánchez^[a], M. Ortiz Domínguez^[a], F. López Sánchez^[a], I. Espinoza Luna ^[b]

Resumen

Se acostumbra estudiar el movimiento de traslación de un objeto en términos de las tres leyes del movimiento de Newton. En este análisis, la fuerza ha jugado un papel central como la cantidad que determina el movimiento. En el presente trabajo, se realiza un análisis alternativo del movimiento de traslación de un sistema masa-resorte sobre un plano inclinado, empleando la segunda ley de Newton y el teorema trabajo-energía. Esto es, en circunstancias bastantes generales, permanecen constantes. El hecho de que existan cantidades que se conservan no sólo nos brinda una compresión más profunda de plantear la resolución de problemas prácticos. Las leyes de conservación de la energía y la cantidad de movimiento son especialmente valiosas al tratar con sistemas de muchos objetos, en los que una relación detallada de las fuerzas implicadas sería difícil, si no es que imposible. Estas leyes son aplicables a un amplio rango de fenómenos, incluidos el mundo atómico y subatómico, donde las leyes de Newton no se aplican.

Palabras clave: Modelo masa-resorte, Principio trabajo-energía, Fuerza conservativa, Fuerza no conservativa, Constante del resorte.

Abstract

It is very common to study the motion of an object in terms of Newton´s laws of motion. In this study, the force has played a central role as the amount that determines the movement. In this paper, an alternative analysis of the motion of a mass-spring system on an inclined plane (slope) is presented, in terms of Newton´s second law and work - energy theorem. This is, in very general circumstances, remain constant. The fact that there are amounts that remain not only gives us a deeper understanding of raising the resolution of practical problems. The laws of conservation of energy and momentum are especially valuable when dealing with systems of many objects, in which a detailed account of the forces involved would be difficult, if not impossible. These laws are applicable to a wide range of phenomena, including the atomic and subatomic world, where Newton's laws do not apply.

Keywords: Mass-spring model, Work-energy principle, Conservative forces, No conservative forces, Spring constant.

1. Introducción

El trabajo realizado contra la gravedad al mover un objeto desde un punto hasta otro no depende de la trayectoria que se siga. Por ejemplo, toma el mismo trabajo (=mgy) elevar a un objeto de masa m verticalmente una cierta altura que llevarlo hacia arriba por un plano inclinado de la misma altura vertical. Las fuerzas como la gravedad, para las que el trabajo efectuado no depende de la trayectoria que se siga, sino sólo de las posiciones inicial y final, se llaman conservativas. La fuerza elástica de un resorte (u otro material elástico) en el que F=-kx , también es una fuerza conservativa. Un objeto que parte en un punto determinado y regresa a ese mismo punto bajo la acción de una fuerza conservativa no tiene trabajo neto aplicado sobre él porque la energía potencial es la misma al principio y al final del trayecto completo. La fuerza de fricción, por otra parte, es una fuerza no conservativa porque el trabajo que realiza depende de la trayectoria. Por ejemplo, cuando una caja se mueve a través de un piso desde un punto a otro, el trabajo realizado depende de si la trayectoria seguida es recta, curva o en zigzag. Asimismo, la energía potencial es energía asociada con la posición o configuración de los objetos, sólo tiene sentido si puede establecer de manera única para un punto dado. Esto no se puede hacer con las fuerzas no conservativas porque el trabajo realizado depende de la trayectoria seguida ^[1-3]. En el presente trabajo de investigación se centra en proporcionar dos métodos de solución de un sistema masa-resorte sobre un plano inclinado, para agilizar los procedimientos de diseño.

2. Trabajo conservativo y no conservativo

La energía potencial sólo se puede definir para una fuerza conservativa. Por eso, aunque la energía potencial siempre está asociada con una fuerza, no todas las fuerzas tienen una energía potencial. Por ejemplo, no existe energía potencial para la fricción. Supongamos que varias fuerzas actúan sobre un objeto que puede experimentar movimiento de traslación. Y supongamos que sólo algunas de esas fuerzas son conservativas. El trabajo total (neto) W_neto será la suma del trabajo realizado por las fuerzas conservativas, y el trabajo realizado por las fuerzas no conservativas,W_nc:

Entonces, a partir del teorema trabajo-energía, se tiene

donde . Entonces

 

El trabajo realizado por una fuerza conservativa se puede expresar en términos de energía potencial:

Al combinar la Ec. (5) con la Ec. (4), se tiene:

Por tanto, el trabajo realizado por las fuerzas no conservativas que actúan sobre un objeto es igual al cambio total en las energías cinética y potencial. Es necesario resaltar que en la Ec. (6) hay que incluir todas las fuerzas que actúan sobre un objeto, ya sea en el término de energía potencial a la derecha (si se trata de una fuerza conservativa) o en el término trabajo a la izquierda (¡pero no en ambos!). Si en un sistema sólo actúan fuerzas conservativas, se llega a una relación particularmente simple y hermosa en la que interviene la energía. Cuando están presentes fuerzas no conservativas, entonces en la Ec. (6), la forma general del teorema trabajo-energía. Así, se tiene:

o

Ahora se define una cantidad , llamada energía mecánica total del sistema, como la suma de las energías cinética y potencial en cualquier momento:

Ahora la Ec. (8), se puede escribir como:

o

La Ec. (10), expresa un principio útil y profundo que tiene que ver con la energía mecánica total de un sistema: que es una cantidad que se conserva. La energía mecánica total permanece constante en tanto no actúen fuerzas no conservativas: ( ) en algún momento inicial 1 es igual a () en cualquier momento ulterior 2. Para decirlo de otra forma, la Ec. (8) sostiene que ; esto es, si la energía cinética de un sistema aumenta, entonces la energía potencial debe disminuir en una cantidad equivalente para compensar. De esta forma, el total , permanece contante:

Si sólo actúan fuerzas conservativas, la energía mecánica total de un sistema no aumenta ni disminuye en ningún proceso. Permanece constante, es decir, se conserva.

Éste es el principio de conservación de la energía mecánica para fuerzas conservativas. En las aplicaciones de la conservación de la energía, en la Ec. (7) se despreció la fricción, una fuerza no conservativa. Pero en muchas situaciones no se puede ignorar. Históricamente, la presencia de las fuerzas disipativas dificultaron la formulación de una ley sobre la conservación de la energía hasta bien entrado el siglo XIX. Sólo entonces fue que el calor, que siempre se produce cuando existe fricción (intente frotar sus manos), se interpretó en términos de energía. Los estudios cuantitativos de los científicos del siglo XIX demostraron que, si el calor se consideraba como una transferencia de energía (térmica), entonces la energía total se conserva en cualquier proceso. La energía térmica producida por una fuerza de fricción constante es igual al trabajo realizado por la fricción ^[1-5]. Ahora se aplica la forma general del principio trabajo-energía:

donde es la distancia sobre la que actúa la fuerza de fricción.

3. Método I

3.1 Ecuación de movimiento

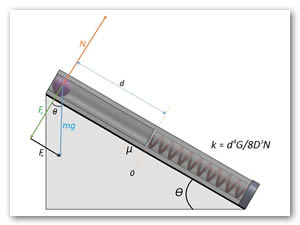
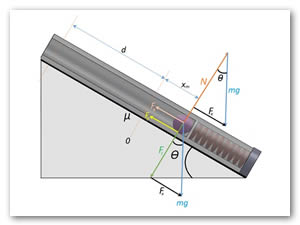
En la Figura 1, se presenta un balín de acero de masa desliza a lo largo de un plano inclinado de ángulo θ. Parte del reposo a una distancia del muelle elástico sin deformar de constante . Calcular la máxima deformación del resorte. Se supone que el plano no es liso, sino que ejerce una fuerza de rozamiento de coeficiente μk sobre el bloque que desliza a lo largo del mismo^[6].

Cuando el balín de acero se mueve hacia abajo ( ), la ecuación del movimiento es (ver Figura 2):

Escribiendo la Ec. (14) en forma de ecuación diferencial, se tiene:

Esta ecuación del movimiento nos recuerda la ecuación diferencial de un Movimiento Armónico Simple, pero además tiene un término adicional . La solución de la ecuación diferencial es la suma de la homogénea (la ecuación de un MAS) más una constante . Introduciendo la solución particular (la constante ) en la ecuación diferencial se tiene:

La solución completa de la ecuación diferencial es:

La velocidad del bloque es:

Los coeficientes y se determinan a partir de las condiciones iniciales. Considerando que el tiempo inicial es cero , el balín de acero llega al origen , con velocidad .

La posición y la velocidad del balín de acero en su movimiento a lo largo del plano inclinado, hacia abajo, es:

El máximo desplazamiento se produce cuando la velocidad es nula , en el instante , de acuerdo con la Ec. (22), se tiene:

Asimismo, se tiene:

Por otro lado sustituyendo la Ec. (24) en la Ec. (21), se tiene:

Reescribiendo la Ec. (25), se tiene:

Considerando las siguientes identidades trigonométricas

Sustituyendo las Ecs. (27) y (28) en la Ec. (26), se obtiene que:

Multiplicando por en ambos lados de la Ec. (30), se llega a:

Reescribiendo la Ec. (31), se obtiene:

Elevando al cuadrado ambos lados de la Ec. (33), se tiene:

Finalmente se obtiene que la compresion máxima del resorte es (ver Figura 2):

4. Método II

4.1 Teorema trabajo-energía

Situando el nivel cero de energía potencial en el origen O, como se observa en la Figura 2. El trabajo de la fuerza de rozamiento es igual a la diferencia entre la energía inicial y la energía final (ver Ec. (12)).

Considerando que la fuerza de fricción es:

donde es la fuerza normal, de la Figura 2, se encuentra que:

Sustituyendo la Ec. (39) en la Ec. (37), se llega a:

 

Sustituyendo la Ec. (40) en la Ec. (36), se encuentra una ecuación de segundo grado para la compresión máxima :

De acuerdo con la solución general de una ecuación cuadrática, se tiene:

5. Resultados y discusiones

Resulta útil contar con una expresión matemática que permita describir la dinámica del sistema masa-resorte sobre un plano inclinado para fines de diseño. Considerando la Ec. (35) ( ), con:

Velocidad inicial

Masa del balín de acero

Constante elástica del resorte

Frecuencia angular

Coeficiente de rozamiento

Ángulo de inclinación del plano inclinado

Aceleración del balín de acero

Posición inicial del balín de acero

La compresión máxima del resorte considerando la Ec. (35), se tiene:

Asimismo, la compresión máxima del resorte considerando la Ec. (44), se tiene:

Las Ecs. (35) y (44) son válidas para describir la dinámica del sistema masa-resorte sobre un plano inclinado.

Conclusiones

Se cuantificó el comportamiento de un sistema masa-resorte sobre un plano inclinado involucrando los parámetros que describen la compresión máxima del resorte ( ), a través de dos métodos de solución. Asimismo, se verificó que en los dos métodos se obtuviera una solución equivalente a través de un ejemplo real.

Agradecimientos

El trabajo descrito en el presente artículo fue financiado por la beca otorgada por PRODEP. Asimismo, los autores le agradecen al Ing. Martín Ortiz Granillo, quien es Director de la Escuela Superior de Ciudad Sahagún-UAEH, México, por todas las facilidades para concluir este trabajo de investigación.

Bibliografía

^[1]Douglas, C. G. (2006). Física, principios con aplicaciones. Volumen I. Estado de México, México: Pearson Education.

^[2]Wilson, D. J. y Buffa, J. A. (2003). Física. Estado de México, México: Pearson Education.

^[3]Joseph W. Kane, E. J. y Sternheim, M. M. (2007). Física. Barcelona, España: Editorial Reverte S. A.

^[4]Kittel, C y Knight, D. W. (2005). Mecánica. Barcelona, España: Editorial Reverte S. A.

^[5]Mendoza, I. V. A., Hernández, G. A. E. y David Piña Reich, P. D. (2014). Física. D. F., México: Grupo Editorial Patria, S. A. de C. V.

^[6]Halliday, D. y Resnick, R. (1980). Física, Parte 1. Estado de México, México: Compañía editorial continental S. A.

^[a]Profesor Investigador de la Escuela Superior de Ciudad Sahagún en la Lic. En Ing. Mecánica-Universidad Autónoma del Estado de Hidalgo

^[b]Alumna de la Licenciatura en Contaduría, en la Escuela Superior de Ciudad Sahagún de la Universidad Autónoma del Estado de Hidalgo, Hidalgo, México.

---

Compartir en: