Análisis del sistema masa-resorte helicoidal.

Martín Ortiz Domínguez^[a]

Resumen

El movimiento oscilatorio de un sistema mecánico, constituye uno de los campos de estudio más importante en Ingeniería Mecánica. Uno de estos sistemas que en varias ocasiones ha sido objeto de estudio, es el sistema conformado por una masa-resorte (oscilador armónico), debido a las diferentes aristas que este presenta. Entre los estudios realizados sobre este sistema, se encuentran aquellos relacionados con los efectos estáticos y dinámicos. En el presenta artículo se presenta un análisis teórico sobre como la constante del resorte (k) en función del diámetro del resorte (D), diámetro de la espira del resorte (d), número de espiras del resorte (N) y el módulo de corte del material (G); afecta la dinámica del sistema

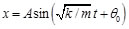
compuesto por una masa que se desplaza sobre una mesa lisa (i.e., sin roce) y la cual está unida a una pared, por medio de un resorte helicoidal.

Palabras clave: Modelo masa-resorte, Grado de libertad, Oscilador armónico, Resorte helicoidal, Ley de Hooke, Constante del resorte, Ecuación diferencial.

Abstract

The oscillatory motion of a mechanical system is one of the most important areas of study in Mechanical Engineering. One of these systems has repeatedly been studied, it is composed of a mass-spring (harmonic oscillator) , due to the different aspects that the system presents. The majority of the studies on this system are those related to static and dynamic effects. In the present study the spring constant (k) of a spring is determinated as a function of the mean coil diameter of the spring (D), wire diameter of the spring (d), number of active coils of the spring (N) and shear modulus of the material (G); to stimate the effects of vibration in the dynamics of mass-spring system

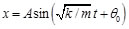
when the mass is moving on a flat table (ie, without friction) and which is attached to a rigid support (wall) by means of a helical spring.

Keywords: Mass-spring model, Degree-of-freedom, Harmonic oscillator, Helical spring, Hooke´s spring law, Spring constant, Differential equation.

1. Introducción

El movimiento oscilatorio se produce porque el sistema tiene la capacidad de volver exactamente a la configuración original y porque existe una fuerza recuperadora que actúa para que lo haga. En el caso del trampolín, al separarlo de la posición de equilibrio, aparece una fuerza recuperadora (de tipo elástico) que tiende a devolverlo a esa posición. Es lo que hace al soltarlo, solo que al llevar una cierta velocidad supera la posición de equilibrio, con lo que, de nuevo, actúa la fuerza recuperadora, pero en sentido opuesto, que tiende a devolverlo a la posición de equilibrio. Y así sucesivamente. El movimiento oscilatorio de vaivén es especialmente sencillo en un caso que llamamos Movimiento Armónico Simple (MAS). Un sistema que se mueve así, también se dice que se comporta como un Oscilador Armónico Simple (OAS).

En física, ¨armónico¨ significa que se describe matemáticamente mediante una función seno o coseno. En el diseño de la mayoría de los elementos mecánicos es deseable, que la deformación inducida por el estado de cargas actualmente sea lo más baja posible. Sin embargo, los resortes mecánicos cumplen en las máquinas la misión de elementos flexibles, sometidos a grandes deformaciones por efecto de cargas externas volviendo a recuperar su forma inicial cuando cesa la acción de las mismas, es decir, presenta una gran elasticidad. Para su fabricación se emplean aceros de gran elasticidad (aceros al carbono, aceros al cromo-vanadio, aceros al cromo-silicio, etc.). Para algunas aplicaciones especiales puede emplearse el cobre endurecido y el latón. Debido al elevado valor de la maquinaria en la industria, los resortes has sido estudiados con mucha meticulosidad. Asimismo, se pueden producir en masa y se han determinado configuraciones ingeniosas para lograr una variedad de propiedades deseadas. Las aplicaciones de los resortes son muy variadas entre las más importantes se puede mencionar las siguientes:

• Como los elementos capaces de absorber energía o cargas de choque, por ejemplo en chasis y topes de ferrocarril.
• Como dispositivos de fuerza para mantener el contacto entre elementos, tal como aparece en los mecanismos de leva y en algunos tipos de embragues.
• En sistemas de suspensión y/o amortiguación, percibiendo la energía instantánea de una acción externa y devolviéndola en forma de energía de oscilaciones elásticas.
• Como elementos motriz o fuente de energía, como en mecanismos de reloj y juguetes, dispositivos de armas deportivas, etc.
• Como elementos capaces de absorber vibraciones.

El objetivo de este trabajo de investigación se centra en proporcionar una expresión matemática que describa el efecto dinámico del sistema masa-resorte helicoidal de sección circular, para agilizar los procedimientos de diseño.

2. Movimiento oscilatorio armónico simple

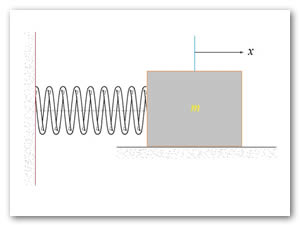
El término armónico se aplica en general a las expresiones que contienen términos con las funciones seno y coseno. Asimismo, se verá, como un movimiento oscilatorio siempre puede ser descrito por estas funciones y al más sencillo de estos movimientos se le denomina: movimiento oscilatorio armónico simple. Para que un bloque realice un movimiento oscilatorio armónico simple debe estar sometida solo a la acción de una fuerza restauradora proporcional al desplazamiento[1-3]. Si se le comunica una energía inicial al bloque se le libera, ejecutará un movimiento de oscilación libre lineal alrededor de la posición de equilibrio. El ejemplo, prototipo o modelo, más sencillo de un oscilador armónico simple es el sistema masa-resorte sujeto a una pared como de presenta en la Figura 1 y teniendo en cuenta las siguientes idealizaciones:

Pared: La pared es rígida y está fija en el espacio.

Masa: El bloque está sometido solo a la acción recuperadora producida por el resorte. No actúa sobre el ningún otro tipo de fuerza, en particular se despreciarán, comparadas con la del resorte, las fuerzas amortiguadoras disipativas de fricción con el apoyo horizontal y la resistividad viscosa del aire.

Resorte helicoidal La masa del resorte helicoidal es despreciable comparada con la masa del bloque, se asume que no tiene masa. No existen fricciones internas o externas en el resorte que produzcan acciones disipativas. La relación elástica de fuerza vs. deformación del resorte es exactamente lineal, es decir, obedece la Ley de Hooke, por lo tanto, las deformaciones del resorte helicoidal deben ser relativamente pequeñas para que no se produzcan efectos permanentes y la relación elástica con la fuerza sea en todo momento estrictamente lineal. A pesar de que se han hecho muchas aproximaciones, como los aspectos esenciales del problema no se han comprometido, la solución de este problema es muy importante y útil pues en muchos casos reales esta aproximación puede dar resultados satisfactorios.

Si la constante de rigidez elástica del resorte es K y el desplazamiento X del bloque se mide a partir de la posición relajada del resorte (sin estirar, ni comprimir), la fuerza restauradora que ejerce sobre el bloque es:

(1)

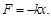
Aplicando la ley de Newton se obtendrá la ecuación diferencial del movimiento del oscilador armónico simple. Igualando la ley de Hooke (F=-kx) con la segunda ley Newton (F=mx), en una dimension se tiene:

(2)

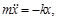
(3)

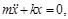
(4)

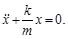
Como m y k son cantidades constantes características del sistema en este caso particular del oscilador masa-resorte y teniendo en cuenta que en la ecuación diferencial aparece el cociente entre ellas (k/m), podemos definir una nueva cantidad constante:

(5)

                                                     

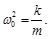
La definición de la Ec. (5), se puede reescribir la Ec. (5) con una sola constante, es decir:

(6)

                                                   

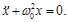
La Ec. (6) corresponde a las llamadas ecuaciones diferenciales ordinarias de segundo orden lineales con coeficientes constantes, que se presentan repetidas veces en el estudio de las Vibraciones Mecánicas [1-13]. Para el caso particular del oscilador armónico simple, se considera a la Ec. (6), es decir:

(7)

                                             

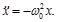
Considerando que la aceleración se puede expresar de la siguiente manera:

(8)

                                                     

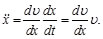
Sustityendo la Ec. (8) en la Ec. (7), se tiene:

(9)

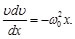
Separando las variables e integrando, se llega a:

(10)

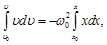
(11)

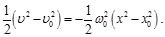
Considerando que en: t=0: x=x₀y v=v₀.Despejando la velocidad de la Ec. (11), se tiene:

(12)

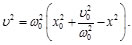
Definiendo que:

(13)

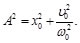
Sustituyendo la ec. (13) en la Ec. (12), se llega a:

(14)

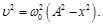
Con la Ec. (14), se tiene que la velocidad se puede expresar en función de la posición (v=f(x)). Volviendo a reescribir la Ec. (14).

(15)

                                                                  

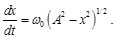
Volviendo a separar las variables e integrar en la Ec. (15), se tiene:

(16)

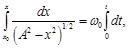
(17)

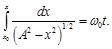
Considerando un cambio de variable en la Ec. (17), es decir:

(18)

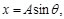
(19)

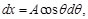
con límites de integración t=0: x=x₀y v=v₀

(20)

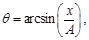
(21)

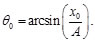
Sustituyendo las Ecs. (18)-(21) en la Ec. (17), se tiene:

(22)

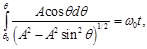
(23)

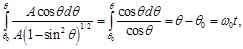
(24)

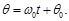
Finalmente sustituyendo la Ec. (24) en la Ec. (18), se llega a:

(25)

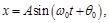
(26)

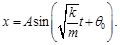
Las cantidades A y 0₀ de acuerdo a las expresiones utilizadas para establecerlas, como puede verse, depende de las condiciones iniciales, es decir de la posición inicial x₀ y de la velocidad inicial v₀ [1-13]. Físicamente se puede decir que es la energía cinética y potencial que se le comunica inicialmente al oscilador para luego liberarlo y que inicie su movimiento oscilatorio. Como la fuerza ejercida por el resorte es consevativa, la energía mecánica total (potencial más cinética) se conserva durante todo el movimiento de oscilación libre.

3. Propiedades elásticas

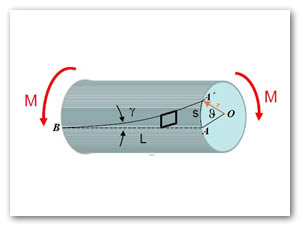
Se pretende determinar la distribución de las deformaciones a cortante en un eje circular de longitud L y radio c que ha sido girado en un ángulo (ver Figura 2). Desprendiendo del eje un cilindro de radio r, la deformación cortante "y" debe ser igual al ángulo ente las líneas AB y A´B (recordar que "y" debe expresarse en radianes). En la Figura 2 se observa que, para valores pequeños de "y", puede expresarse la logitud de arco AA´ como AA´=Ly. Pero, por otra parte, se tiene que AA´=r. Se deduce que:

(27)

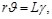
(28)

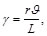
donde "y" y están, ambos expresados en radianes. La Ec. (28) muestra, como podría haberse anticipado, que la deformación a cortante en un punto dado del eje en torsion es proporcional al ángulo de giro AA´=r. También muestra que "y" es proporcional a la distancia "r" desde el eje de la fleche hasta el punto bajo consideración. Por lo tanto, la deformación unitaria a corte en una flecha circular varía linealmente con la distancia desde el eje de la flecha. Se deduce de la Ec. (28) que expresa la deformación a cortante es máxima en las superficie del eje, donde r=c. Se tiene:

(29)

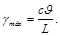
Combinando las Ecs. (28) y (29), puede expresarse la deformación a cortante "y" a una distancia "r" del eje de la fleche como:

(30)

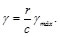
4. Esfuerzos en el rango elástico

Considerar el caso en el que el par torsión M es tal que todos los esfuerzos cortantes en el eje se encuentran por debajo de la resistencia a la cedencia o_r, esto significa que los esfuerzos en el eje permanecerán por debajo del límite de proporcionalidad y también por debajo del límite elástico. Por lo tanto, se aplicará la ley de Hooke y no habrá deformación permanente. Aplicando la ley de Hooke par el esfuerzo y la deformación a cortante, se escribe:

(31)

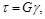
donde G es el módulo de rigidez o modulo de corte del material. Multiplicando ambos miembros de la Ec. (30) por G se escribe:

(32)

                                                                  

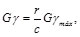
o, considerando la Ec. (31), se llega a que la Ec. (32), se puede expresar como:

(33)

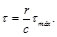
La Ec. (33), muestra que, mientras la resistencia a la cedencia (o el límite de proporcionalidad) no sea excedida en ninguna parte de la fleche circular, el esfuerzo cortante en la fleche varía linealmente con la distancia "r" desde el eje de la flecha. La magnitud del par torción M ejercido sobre el eje:

(34)

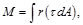
con dF=rDA. Sustituyendo la Ec. (31) en la Ec. (34), se llega a:

(35)

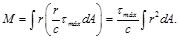
La integral en el ultimo miembro representa el momento polar de inercia de la sección transversal con respecto a su centro O. Se tiene entonces que

(36)

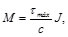
donde esfuerzo cortante máximo se puede expresar como:

(37)

                                                       

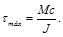
Finalmente sustituyendo la Ec. (37) en la Ec. (33), se expresa el momento cortante a cualquier distancia "r" del eje de la flecha como:

(38)

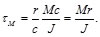
5. Esfuerzos en resortes helicoidales

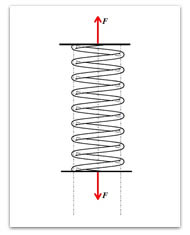
La Figura 3 representa un resorte helicoidal de espiras cerradas, estirado bajo la acción de una fuerza axial F.

El resorte está formado por un alambre o varilla redonda de diámetro "r" enrollada en forma de hélice de radio medio R(=D/2). La pendiente de esta hélice es pequeña, de manera que se puede considerar can bastante aproximación que cada espira está situada en un plano perpendicular al eje del resorte. Para determiner los esfuerzos producidos por F se sigue el procedimiento general de cortar el resorte por una sección de exploración, y determinar las fuerzas resistentes que se necesitan para el equilibrio de una de las porciones separadas por esta sección. Después se analiza la distribución de esfuerzos que originan estas fuerzas resistentes. La Figura 4 representa el diagrama de cuerpo libre de la porción superior del resorte. Para el equilibrio en dirección axial, la fuerza F, que representa la acción sobre esta sección de la porción suprimida, ha de ser igual a F.

El equilibrio horizontal también se cumple, ya que ninguna de las dos, ni F ni F, tienen componentes en esta dirección. Para el equilibrio de momentos, como F y F, opuestas y paralelas, producen un par M=FR, en la sección debe existir otro par resistente M=FR igual y opuesto al anterior, originado por un esfuerzo cortante de torsion, distribuido en la sección de corte. Se representa por M=FR.

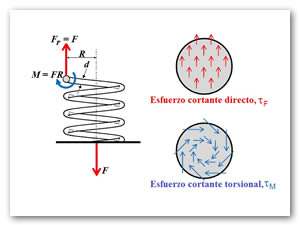
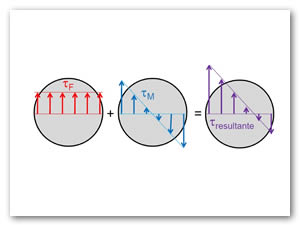
En la Figura 4, se presenta la distribución de esfuerzos que producen estas fuerzas resistentes en la sección de corte. Observamos dos tipos de esfuerzo cortante: (1) un esfuerzo cortante uniformemente distribuido, producido por la fuerza resistente F que pasa su centro de gravedad, y (2) un esfuerzo cortante variable producido por el par torsor resistente determinado en la Ec. (38). Este ultimo varía tanto en magnitude, con la distancia al centro, como en dirección, ya que es perpendicular al radio en cada punto. El esfuerzo resultante en cada punto es la suma de y (ver Figura 5).

En resumen, el esfuerzo cortante máximo tiene lugar en el punto de la sección más próximo al eje del resorte y viene dado por la suma del esfuerzo cortante directo, =F/Ay =Mr/J[1], es decir:

(39)

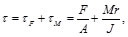
donde,

(40)

                                                      

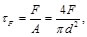
(41)

                                                       

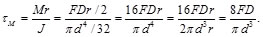
Sustituyendo las Ecs. (40) y (41) en la Ec. (39), se tiene:

(42)

  

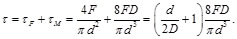
6. Deformación en resortes helicoidales y el efecto en la curvatura

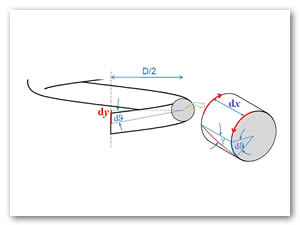
Prácticamente toda la elongación de un resorte según el eje se debe a la torsión del alambre. En la Figura 6, se presenta la deformación de un resorte helicoidal.

                                                             

De la Figura 7, se tiene:

(43)

                                                    

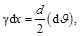
donde

(44)

                                                       

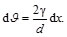
Por otro lado, se tiene que el arco "dy" se puede expresar como: 

(45)

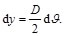
Sustituyendo la Ec. (44) en la Ec. (45), se llega:

(46)

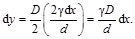
La elongación total es la suma de todas las contribuciones "dy":

(47)

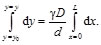
donde L=NπD es la longitud del resorte. Por lo que la Ec. (47), escribe como:

(48)

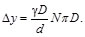
Además, de la Ec. (31) se tiene:

(49)

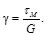
Sustituyendo las Ecs. (41) y (49) en la Ec. (48), se tiene:

(50)

                                                       

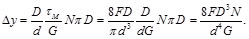
Y la constante elástica o rigidez del resorte helicoidal resulta en:

(51)

                                     

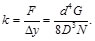
Finalmente sustituyendo la Ec. (51) en la Ec. (26), se llega a una expresión que considera las dimensiones del resorte y el módulo de corte del material, es decir:

(52)

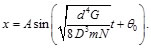
7. Resultados y discusiones

Resulta útil contar con una expresión matemática (ver Ec. (52)) que permita describir la dinámica del sistema masa-resorte para fines de diseño. Asimismo, es muy importante señalar que la Ec. (52) no con contempla la masa del resorte, Arrieta A. et al [13] realizaron un estudio teórico-experimental sobre el efecto dinámico que la masa del resorte tiene sobre las oscilaciones del sistema, encontraron que: La masa del resorte si tiene un efecto sobre la dinámica del sistema (más apreciable será cuanto más despreciable sea la masa (m) que está unida al resorte) en comparación con la suya. En la mayoría de los casos, para aquellos resortes livianos y no tan rígidos, la Ec. (52) es válida para describir la dinámica del sistema masa-resorte.

Conclusiones

 

Una vez hecho el estudio teórico del efecto dinámico del sistema masa-resorte helicoidal sobre las oscilaciones en un solo grado de libertad, se encontró que:

                 

• La constante del resorte ( 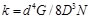) se puede expresar en términos del diámetro del resorte (D), diámetro de la espira del resorte (d), número de espiras del resorte (N) y el módulo de corte del material (G).
• Se determinó una expresión matemática que describe la configuración del sistema masa-resorte helicoidal de sección circular ( 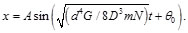),que minimiza los procedimientos de diseño.

Agradecimientos

El trabajo descrito en el presente artículo fue financiado por la beca otorgada por PROMEP. Asimismo, le agradezco al Ing. Martín Ortiz Granillo, quien es Director de la Escuela Superior de Ciudad Sahagún-UAEH, México, por todas las facilidades para concluir este trabajo de investigación

Referencias

1. Rao, S. S. (2012). Vibraciones Mecánicas. D. F. México: Pearson Education.

2. Sofronas, A. (2012). Case Histories in Vibration Analysis and Metal Fatigue for the Practicing Engineer. N. J. USA: John Wiley and Sons, Inc.

3. Russell Johnston E. R., DeWolf J. T. y Mazurek F. D. (2012). Mecánica de Materiales. D. F., México. Mc Graw Hill Education.

4. Nunes da Silva J. M., (1994), Renormalized vibrations of a loaded spring. Am. J. Phys. 62 (5), 423-426.

5. Christensen, J., (2004), An improved calculation of the mass for the resonant spring pendulum. Am. J. Phys. 72 (6), 721-848.

6. Galloni, E. E., Kohen, M., (1979), Influence of the mass of the spring on its static and dynamic effects. Am. J. Phys. 47 (12), 1076- 1078.

7. Heard, T. C., Newby, N. D., (1977), Behavior of a soft spring. Am. J. Phys. 45 (11), 1102-1106.

8. Cushing, J. T., (1984), The Spring-mass system revisited. Am. J. Phys. 52 (10), 925-937.

9. Weinstock, R., (1964), Spring-mass correction in uniform circular motion. Am. J. Phys. 32 (5), 370-376.

10. Weinstock, R., (1964), Oscillations of a particle attached to a heavy spring: An application of the Stieltjes integral. Am. J. Phys. 47(6), 508-514.

11. McDonald, F. A., (1980), Deceptively simple harmonic motion: A mass on a spiral spring. Am. J. Phys. 48 (3), 189-192.

12. Bowen, J. M., (1982), Slinky oscillations and the motion of effective mass. Am. J. Phys. 50 (12), 1145-1148.

13. Arrieta, A., Arrieta, E. S., Tejeiros, J. M., (2009), Masa Efectiva para un Sistema de Muelle Real. Revista Colombiana de Física. 41 (2), 517-519.

14. Deformación unitaria cortante. Recuperado el 20 de marzo de 2015, de http://ocw.uc3m.es/ingenieria-mecanica/elementos-de-maquinas/material-de-clase-1/teoriaresortes.pdf.

15. Resorte helicoidal de espiras cerradas. Recuperado el 20 de marzo de 2015, de http://ocw.uc3m.es/ingenieria-mecanica/elementos-de-maquinas/material-de-clase-1/teoriaresortes.pdf.

16. Diagrama de cuerpo libre. Recuperado el 20 de marzo de 2015, de http://ocw.uc3m.es/ingenieria-mecanica/elementos-de-maquinas/material-de-clase-1/teoriaresortes.pdf.

17. Suma de las dos distribuciones, producen un capo torsional descentrado. Recuperado el 20 de marzo de 2015, de http://ocw.uc3m.es/ingenieria-mecanica/elementos-de-maquinas/material-de-clase-1/teoriaresortes.pdf.

18. Deformación de un resorte helicoidal. Recuperado el 20 de marzo de 2015, de http://ocw.uc3m.es/ingenieria-mecanica/elementos-de-maquinas/material-de-clase-1/teoriaresortes.pdf.

                                                                                                                                 

[1]El momento polar de inercia para un círculo de radio c es: J = πc4/2.

^[a] Profesor Investigador de la Universidad Autónoma del Estado de Hidalgo.